|
|
| Со скольки лет надо начинать изучать математику? |
|
|
|
|
|
|
|
Все в этом мире меняется. То, что наши предшественники могли понять только к двадцати годам, люди сейчас понимают уже в 15 и ранее. Современный мир таков, что все молодеет.
|
|
|
|
|
|
|
|
| Зачем нам изучать математику? Почему именно математика? |
|
|
|
|
|
|
|
Математика - это одна из тех наук, основы, которой была заложены не год, не два и даже не сто лет назад. Математика с нами уже несколько тысяч лет.
|
|
|
|
|
|
|
|
| Писать шпаргалки или не писать? |
|
|
|
|
|
|
|
"Писать шпаргалки или не писать?" - вот в чём вопрос. Математика - предмет серьёзный и решение задач требует хорошего знания формул. Поэтому, ответ теоретиков и учащихся - писать стоит.
|
|
|
|
|
|
|
|
| Шпаргалки не для нас |
|
|
|
|
|
|
|
Как известно из многих источников есть цвета, которые очень хорошо располагают к себе человека, действуя на подсознание человека, это голубой и зеленый цвет. Вот в таких тонах и желательно одеваться на экзамен.
|
|
|
|
|
|
|
|
| Математика - часть нашей жизни |
|
|
|
|
|
|
|
Не раз приходилось слышать фразу о том, что математика - страна без границ. Несмотря на свою банальность, фраза о математике имеет под собой очень веские основания. Математика в жизни человека занимает особое место.
|
|
|
|
|
|
|
|
| Математика в решении строительных задач |
|
|
|
|
|
|
|
Математика используется повсеместно, для решения задач из самых разных областей. В том числе, и для решения задач строительства.
|
|
|
|
|
|
|
|
| Подготовка к контрольной работе, концентрация |
|
|
|
|
|
|
|
Контрольная работа, это отличный способ проверить свои знания и навыки, полученные за время обучения. Контрольные работы по математике отличаются повышенной сложностью.
|
|
|
|
|
|
|
|
| Решение задач и оформление контрольных работ по дисциплине математика |
|
|
|
|
|
|
|
Все большее количество людей, сейчас предпочитают учиться удаленно, таким образом нужно уделять много внимания правильному оформлению сделанных контрольных работ.
|
|
|
|
|
|
|
|
|
|
Как найти ошибку в софизме? Примеры софизмов Подготовил Бакушкин Иван
Как найти ошибку в софизме?
Зачастую найти ошибку в софизме очень сложно. К тому же не существовал алгоритм нахождения ошибки в софизме. Но я, проанализировав софизмы, составил алгоритм, который может помочь в нахождении ошибки во многих софизмах.
- Внимательно прочитать условие предложенной вам задачи
(Начинать поиск ошибки лучше с условия предложенного софизма. В некоторых софизмах абсурдный результат, получается, из-за противоречивых или неполных данных в условии, неправильного чертежа, ложного первоначального предположения, а далее все рассуждения проводятся верно. Это и вызывает затруднения при поиске ошибки)
- Установить темы, которые отражены в софизме
(Ученики, учителя привыкли, что задания, предполагаемые в учебнике, не содержат ошибок в условии и, поэтому, если получается неверный результат, то ошибку они ищут непременно по ходу решения)
- Воспроизвести вслух точные формулировки утверждений
(Установить темы, которые отражены в софизме, предложенных преобразованиях. Софизм может делиться на несколько тем, которые потребуют детального анализа каждой из них. И если вы увидели эти темы, попытайтесь зрительно разбить «большой софизм» на маленькие)
- Выяснить, соблюдены ли все условия применимости теорем, правил, формул, логичности
(Воспроизвести вслух точные формулировки утверждений, используемых в софизме. Например: 2 * 2 =5. Если произнести эту фразу вслух, то мы можем услышать ошибку, услышав самого себя, или более подробно разобраться в смысле софизма)
- Проверять преобразования. После каждого перехода проверить полученный результат обратным действием
(Выяснить, соблюдены ли все условия применимости теорем, правил, формул, соблюдена ли логичность. Действительно, некоторые софизмы построены на неверном использовании определений, законов, на «забывании» условий применимости некоторых теорем. Очень часто в формулировках, правилах запоминаются основные, главные фразы и предложения, всё остальное упускаются. И тогда второй признак равенства треугольников превращается в признак «по стороне и двум углам»)
- Следует разбить работу на небольшие блоки и проконтролировать правильность каждого такого блока
(Работать блоками. Следует разбить работу на небольшие блоки и проконтролировать правильность каждого такого блока. Удобнее проследить за одним блоком, чем за целым преобразованием)
Примеры софизмов
- «Двусмысленность произношения»
Сто сорок да сто сорок будет двести сорок.
- «Рассуждение о женщинах»

Translate\Перевод
- Если у вас будет женщина, то вам потребуется время и деньги:
a. Женщина=Время*Деньги
- Время-деньги, поэтому:
a. Время=Деньги
- Из этого следует:
a. Женщина=Деньги*Деньги
b. Женщина=Деньги в квадрате
c. Деньги- это и есть все ваши проблемы:
d. Деньги=Корень из проблем
i. Из этого следует:
ii. Женщина=Корень из проблем в квадрате
Вывод: Женщина=ПРОБЛЕМЫ
- «Апельсин- планета»
Земля, Марс ит. д. - круглые. Значит, все планеты круглые. Апельсин тоже круглый, значит апельсин – планета.
- «Нет конца»
Движущийся предмет должен дойти до половины своего пути прежде, чем он достигнет его конца. Затем он должен пройти половину оставшейся половины, затем половину этой четвертой части и т.д. до бесконечности. Предмет будет постоянно приближаться к конечной точке, но так никогда ее не достигнет.
- «Продолжительность учебного года»
Можно доказать, что учителя и ученики целый год ничего не делают.
Для простоты будем считать, что в году 360 дней, из них 52 воскресных дня. Если не считать других выходных дней, останется 308 учебных дней. Ночью школа не работает, следовательно, половина количества суток пропадает, остается 154 учебных дня. В большинстве школ занятия продолжаются только до полудня, вследствие чего учебное время уменьшается вдвое. Получаем 77 учебных дней. Будем считать, что на каникулы выпадает только 60 дней, тогда для занятий останется всего 17 дней в году.
- «Песенка английских студентов»
Чем больше учишься, тем больше знаешь.
Чем больше знаешь, тем больше забываешь.
Чем больше забываешь, тем меньше знаешь.
Чем меньше знаешь, тем меньше забываешь.
Но чем меньше забываешь, тем больше знаешь.
Так для чего учиться?
- « Единица равна нулю»
Возьмем уравнение
х-а = 0
Разделив обе его части на х-а, получим
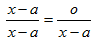
Откуда сразу же получаем требуемое равенство
1=0
Ошибка заключается в том, что на 0 делить нельзя (1).
- «Семь равно тринадцати»
Рассмотрим уравнение
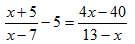
Оно может быть решено следующим образом. Приведя левую часть уравнения к общему знаменателю, будем иметь
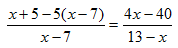
Откуда следует
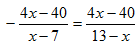
или
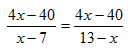
Поскольку числители дробей в левой и правой частях уравнения равны, то для того чтобы имело место равенство обеих частей уравнения, необходимо, чтобы были равны и знаменатели дробей. Таким образом, приходим к равенству
7=13
Ошибка состоит в том, что область допустимых значений исходного уравнения (1) состоит из всех значений переменой х кроме х=7, х=13. В этом софизме неявно подразумевается, что равенство(2) является не уравнением, а тождеством равным при любых значениях х, что неверно. Поэтому утверждение софизма не имеет места.
- «Один рубль не равен ста копейкам»
Возьмем верное равенство:
1 р. = 100 к.,
Возведем его по частям в квадрат, получим:
1 р. = 10000 к.
Таким образом, один рубль не равен ста копейкам.
(Ошибка: умножение величины на себя не имеет смысла, в квадрат возводятся только числа).
- «2x2=5»
Найти ошибку в рассуждении: Имеем верное числовое равенство: 4:4=5:5.
Вынесем за скобки в каждой части его общий множитель. Получим: 4(1:1)=5(1:1).
Числа в скобках равны, поэтому 4=5 или .
(Ошибка: ошибка допущена в левой и правой частях тождества 4:4=5:5 при вынесении общего множителя за скобки.)
|